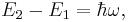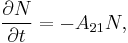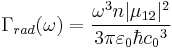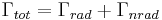Spontaneous emission
Spontaneous emission is the process by which a light source such as an atom, molecule, nanocrystal or nucleus in an excited state undergoes a transition to a state with a lower energy, e.g., the ground state and emits a photon. Spontaneous emission of light or luminescence is a fundamental process that plays an essential role in many phenomena in nature and forms the basis of many applications, such as fluorescent tubes, older television screens (cathode ray tubes), plasma display panels, lasers (for startup - normal continuous operation works by stimulated emission instead) and light emitting diodes.
Contents |
Introduction
If a light source ('the atom') is in the excited state with energy 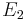 , it may spontaneously decay to a lower lying level (e.g., the ground state) with energy
, it may spontaneously decay to a lower lying level (e.g., the ground state) with energy 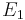 , releasing the difference in energy between the two states as a photon. The photon will have angular frequency
, releasing the difference in energy between the two states as a photon. The photon will have angular frequency  and energy
and energy 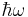 (=
(= 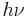 , where
, where  is the Planck constant and
is the Planck constant and  is the frequency):
is the frequency):
where 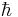 is the reduced Planck constant. The phase of the photon in spontaneous emission is random as is the direction the photon propagates in. This is not true for stimulated emission. An energy level diagram illustrating the process of spontaneous emission is shown below:
is the reduced Planck constant. The phase of the photon in spontaneous emission is random as is the direction the photon propagates in. This is not true for stimulated emission. An energy level diagram illustrating the process of spontaneous emission is shown below:
If the number of light sources in the excited state is given by  , the rate at which
, the rate at which  decays is:
decays is:
where  is the rate of spontaneous emission. In the rate-equation
is the rate of spontaneous emission. In the rate-equation  is a proportionality constant for this particular transition in this particular light source. The constant is referred to as the Einstein A coefficient, and has units
is a proportionality constant for this particular transition in this particular light source. The constant is referred to as the Einstein A coefficient, and has units 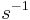 .[1] The above equation can be solved to give:
.[1] The above equation can be solved to give:
where  is the initial number of light sources in the excited state,
is the initial number of light sources in the excited state,  is the time and
is the time and 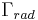 is the radiative decay rate of the transition. The number of excited states
is the radiative decay rate of the transition. The number of excited states  thus decays exponentially with time, similar to radioactive decay. After one lifetime, the number of excited states decays to 36.8% of its original value (
thus decays exponentially with time, similar to radioactive decay. After one lifetime, the number of excited states decays to 36.8% of its original value (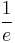 -time). The radiative decay rate
-time). The radiative decay rate 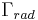 is inversely proportional to the lifetime
is inversely proportional to the lifetime 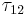 :
:
Theory
Spontaneous transitions was not explainable within the framework of the old quantum theory, that is a theory in which the atomic levels are quantized, but the electromagnetic field is not. In fact, using the machinery of the usually called "first-quantized" quantum mechanics and one computes the probability of spontaneous transitions from one stationary state to another, one finds that it is zero. In order to explain spontaneous transitions, quantum mechanics must be extended to a "second-quantized" theory, wherein the electromagnetic field is quantized at every point in space. Such a theory is known as a quantum field theory; the quantum field theory of electrons and electromagnetic fields is known as quantum electrodynamics.
In quantum electrodynamics (or QED), the electromagnetic field has a ground state, the vacuum state, which can mix with the excited stationary states of the atom (for more information, see Ref. [2]). As a result of this interaction, the "stationary state" of the atom is no longer a true eigenstate of the combined system of the atom plus electromagnetic field. In particular, the electron transition from the excited state to the electronic ground state mixes with the transition of the electromagnetic field from the ground state to an excited state, a field state with one photon in it. Spontaneous emission in free space depends upon vacuum fluctuations to get started.[2][3]
Although there is only one electronic transition from the excited state to ground state, there are many ways in which the electromagnetic field may go from the ground state to a one-photon state. That is, the electromagnetic field has infinitely more degrees of freedom, corresponding to the different directions in which the photon can be emitted. Equivalently, one might say that the phase space offered by the electromagnetic field is infinitely larger than that offered by the atom. Since one must consider probabilities that occupy all of phase space equally, the combined system of atom plus electromagnetic field must undergo a transition from electronic excitation to a photonic excitation; the atom must decay by spontaneous emission. The time the light source remains in the excited state thus depends on the light source itself as well as its environment. Imagine trying to hold a pencil upright on the end of your finger. It will stay there if your hand is perfectly stable and nothing perturbs the equilibrium. But the slightest perturbation will make the pencil fall into a more stable equilibrium position. Similarly, vacuum fluctuations cause an excited atom to fall into its ground state.
In spectroscopy one can frequently find that atoms or molecules in the excited states dissipate their energy in the absence of any external source of photons. This is not spontaneous emission, but is actually nonradiative relaxation of the atoms or molecules caused by the fluctuation of the surrounding molecules present inside the bulk.
Rate of spontaneous emission
The rate of spontaneous emission (i.e., the radiative rate) can be described by Fermi's golden rule.[4] The rate of emission depends on two factors: an 'atomic part', which describes the internal structure of the light source and a 'field part', which describes the density of electromagnetic modes of the environment. The atomic part describes the strength of a transition between two states in terms of transition moments. In a homogeneous medium, such as free space, the rate of spontaneous emission in the dipole approximation is given by:
where  is the emission frequency,
is the emission frequency,  is the index of refraction,
is the index of refraction,  is the transition dipole moment,
is the transition dipole moment, 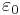 is the vacuum permittivity,
is the vacuum permittivity, 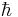 is the reduced Planck constant and
is the reduced Planck constant and 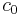 is the vacuum speed of light. (This approximation breaks down in the case of inner shell electrons in high-Z atoms.) Clearly, the rate of spontaneous emission in free space increases with
is the vacuum speed of light. (This approximation breaks down in the case of inner shell electrons in high-Z atoms.) Clearly, the rate of spontaneous emission in free space increases with 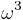 . In contrast with atoms, which have a discrete emission spectrum, quantum dots can be tuned continuously by changing their size. This property has been used to check the
. In contrast with atoms, which have a discrete emission spectrum, quantum dots can be tuned continuously by changing their size. This property has been used to check the 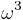 -frequency dependence of the spontaneous emission rate as described by Fermi's golden rule.[5]
-frequency dependence of the spontaneous emission rate as described by Fermi's golden rule.[5]
Radiative and nonradiative decay: the quantum efficiency
In the rate-equation above, it is assumed that decay of the number of excited states  only occurs under emission of light. In this case one speaks of full radiative decay and this means that the quantum efficiency is 100%. Besides radiative decay, which occurs under the emission of light, there is a second decay mechanism; nonradiative decay. To determine the total decay rate
only occurs under emission of light. In this case one speaks of full radiative decay and this means that the quantum efficiency is 100%. Besides radiative decay, which occurs under the emission of light, there is a second decay mechanism; nonradiative decay. To determine the total decay rate 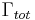 , radiative and nonradiative rates should be summed:
, radiative and nonradiative rates should be summed:
where 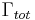 is the total decay rate,
is the total decay rate, 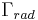 is the radiative decay rate and
is the radiative decay rate and 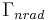 the nonradiative decay rate. The quantum efficiency (QE) is defined as the fraction of emission processes in which emission of light is involved:
the nonradiative decay rate. The quantum efficiency (QE) is defined as the fraction of emission processes in which emission of light is involved:
In nonradiative relaxation, the energy is released as phonons, more commonly known as heat. Nonradiative relaxation occurs when the energy difference between the levels is very small, and these typically occur on a much faster time scale than radiative transitions. For many materials (for instance, semiconductors), electrons move quickly from a high energy level to a meta-stable level via small nonradiative transitions and then make the final move down to the bottom level via an optical or radiative transition. This final transition is the transition over the bandgap in semiconductors. Large nonradiative transitions do not occur frequently because the crystal structure generally can not support large vibrations without destroying bonds (which generally doesn't happen for relaxation). Meta-stable states form a very important feature that is exploited in the construction of lasers. Specifically, since electrons decay slowly from them, they can be piled up in this state without too much loss and then stimulated emission can be used to boost an optical signal.
See also
- Absorption (optics)
- Stimulated emission
- Emission spectrum
- Spectral line
- Atomic spectral line
- Laser science
- Purcell effect
- Photonic crystal
- Vacuum Rabi oscillation
- Jaynes-Cummings model
References
- ^ R. Loudon, The Quantum Theory of Light, 3rd ed. (Oxford University Press Inc., New York, 2001).
- ^ Hiroyuki Yokoyama & Ujihara K (1995). Spontaneous emission and laser oscillation in microcavities. Boca Raton: CRC Press. p. 6. ISBN 0849337860. http://books.google.com/books?id=J_0ZAwf6AQ0C&printsec=frontcover&dq=%22spontaneous+emission%22#PPA6,M1.
- ^ Marian O Scully & M. Suhail Zubairy (1997). Quantum optics. Cambridge UK: Cambridge University Press. p. §1.5.2 pp. 22–23. ISBN 0521435951. http://books.google.com/books?id=20ISsQCKKmQC&pg=PA430&dq=atom+transition+photon#PPA22,M1.
- ^ B. Henderson and G. Imbusch, Optical Spectroscopy of Inorganic Solids (Clarendon Press, Oxford, UK, 1989).
- ^ A. F. van Driel, G. Allan, C. Delerue, P. Lodahl,W. L. Vos and D. Vanmaekelbergh, Frequency-dependent spontaneous emission rate from CdSe and CdTe nanocrystals: Influence of dark states, Physical Review Letters, 95, 236804 (2005).http://cops.tnw.utwente.nl/pdf/05/PHYSICAL%20REVIEW%20LETTERS%2095%20236804%20(2005).pdf